雨夜带刀

最近碰到的一个需求需要借助字符串的快速搜索算法，于是看了一些有关字符串搜索的一些算法，最先看的是 KMP 算法，看完之后发现还有更优的算法，那就是 Boyer Moore 算法。编辑器的文本搜索、GNU 的 grep 都有使用 Boyer Moore 算法，那么效率应该是经过权威验证的。

虽然网上有不少介绍资料，但我还是从一个算法小白所理解的算法原理来尝试解析该算法，算法大神可绕道了。

从头至尾搜索一个字符串，看这个被搜索的字符串是否包含指定的子串，有则返回其位置，没有则返回 -1，相当于使用自己的算法来实现 JavaScript 中的 String.prototype.indexOf 的功能。

在接下来的讲解中使用 text 来代指被搜索的字符串，pattern 代指用于搜索的子串。

先来看第一个例子：

Boyer Moore 算法的匹配方式是从 pattern 的末尾开始的，如果 pattern 的末尾和 text 不匹配，那么就可以判定它们不匹配。

图一中 pattern 的字符「e」和 text 中的「s」不匹配，那么将 pattern 往右移，移多少位呢？上面说了 Boyer Moore 算法的匹配是从末尾匹配的，由于末尾起的第一个字符就不匹配，并且 text 对应的「s」也没有出现在 pattern 中，那么在「s」之前的所有字符串肯定都是不匹配的，此时将 pattern 往右移动到其开始位置刚好在 text 中的「s」之后。

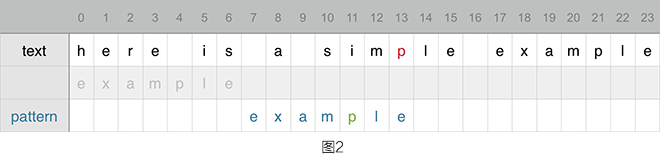
在图二中 pattern 已经右移到了 text 中的「s」之后，此时仍然从末尾开始匹配，text 中的「p」与 pattern 中的「e」不匹配。但是 text 中的「p」有在 pattern 出现过，这是可能匹配的特征之一，那么此时将 pattern 继续往右移，这个时候从图中很直观的可以看出，pattern 应该尝试将自己包含的「p」与 text 中的刚刚进行匹配的「p」对齐，那么 pattern 应该向右移动 2 位才能确保「p」刚好对齐。

这种位移规则总结起来就是坏字符规则，坏字符是相对于 text 来说的，当从末尾开始匹配时发现 text 中的字符和 pattern 不匹配，那么 text 中不匹配的那个字符就是坏字符。匹配到坏字符时，要检查坏字符是否有在 pattern 中出现过，如果没有出现过，那么得将 pattern 位移到坏字符之后，如果出现过，那么位移的位数就是将 pattern 中出现的字符与 text 中的坏字符对齐。

那如果坏字符在 pattern 中出现过多次呢，该以哪个为准？因为匹配顺序是从末尾开始的，也可以说是从右往左，那么其出现的位置也应该从右往左开始查找，第一个（最右）的就是。这种查找规则就是 lastIndexOf 的查找规则。

坏字符移动位数的计算规则就是：

• 移动位数 = pattern 匹配到坏字符的位置 – 坏字符在 pattern 中的位置

如果坏字符没有在 pattern 出现过，那么其位置就是 -1。根据以上的规则，图一中 pattern 匹配到坏字符的位置对应的字符是「e」，坏字符并未在 pattern 中出现过，那么移动位数就是「e」的位置 6 – (-1)，为 7。
到了图二， pattern 匹配到坏字符的位置对应的字符仍然是「e」，坏字符出现的位置为 4，那么移动位数就是「e」的位置 6 – 4，为 2。

根据坏字符规则再来看另一个例子：

直接从第二步开始看，text 中的坏字符「b」与 pattern 最右边的「b」匹配上了，如果按照坏字符规则的计算，那么其计算结果为 1 – 2，为 -1，移动位置往左移动了一位，这不科学啊，不可能往左移，那么如果碰到这种往左移的情况就可以保守的将 pattern 往右移 1 位即可。

再回到第一个例子，此时应该往右移动 2 位。

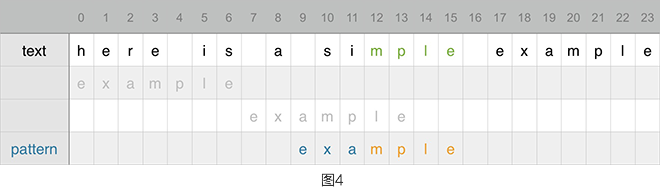
继续从末尾开始匹配，发觉其中的「mple」都能正好匹配，而如果继续匹配的话，text 中的「i」和 pattern「a」是不匹配的。按照坏字符的计算，其移动位置应该是「a」的位置 2 – (-1)，为 3，「i」并未在 pattern 中出现过。

因为上面有提到「mple」都能正好匹配，是否存在更好的位移规则呢。「mple」正好能匹配，那么称其为好后缀，好后缀是相对于 pattern 来说的，从图中可以隐隐的看出貌似有更好的位移规则。继续往下推导。

对于一个字符串来说，除了第一个字符以外，其后所有字符的组合都能称其为后缀。拿 example 来说，就会有后缀「xample」「ample」「mple」「ple」「le」「e」, pattern 和 text 从末尾开始匹配，匹配上的都称为好后缀。那么对于好后缀来说，该如何移动呢？

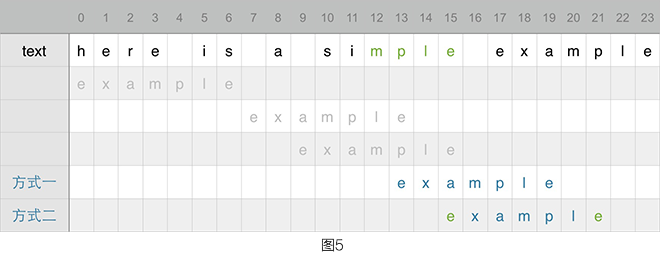
图五中，假如末尾了 4 个后缀，那么是否可以尝试将其移动 4 位呢？答案是肯定的，方式一就是位移结果，慢着好像还有更好的方法。「mple」在 pattern 整个后缀并没有再次出现过，而如果将 pattern 按照好后缀进行拆分后就成为了「exa」和「mple」,而「exa」和「mple」根本无法完全匹配，那么从图中直观的来看 pattern 和 text 并没有一个能相互对应上的位置。上面提到过「e」也是后缀，并且其包含在「mple」中，那么此时将左边的「e」移动到原来右边的「e」所在的位置，此时 pattern 和 text 有相互对应的关系，图五种的方式二比方式一可以多移 2 位，更优，并且这种位移方法也是切实可行的。

坏字符的位移比较容易看懂，而好后缀的位移规则可能要复杂些。对于好后缀「mple」来说，其可以再分解成 3 个「ple」「le」「e」，这样子分解后会发觉只有「e」在 pattern 有重复出现过，如果好后缀在这样分解后发觉某个好后缀有重复出现过，那么此时的位移就以重复出现过的好后缀为准。如果分解后的好后缀还没有在 pattern 种出现过，只能退而求其次，按照方式一来移动。

假如 pattern 为 bcabab 恰好其好后缀是「ab」,而「ab」还可以拆分成「b」,此时到底以哪个好后缀为准呢？其实这种情况下，不管是「ab」还是「b」为准，其位移的位数都是一样的。

那么来总结下好后缀的位移的计算规则：

• 移动位数 = 好后缀在 pattern 中出现的位置 – 好后缀在 pattern 中的重复出现的位置

其重复出现的位置也和坏字符的位置规则一样从右往左开始找，第一个（最右）就是。

那么什么时候该使用好后缀，什么时候该用好后缀？这要看两种规则，哪种能移动更多的位数。

上面的例子继续往右移，这个时候根据坏后缀规则，仅移动 2 位就能完全匹配了。至此就找出了完全匹配的位置了。

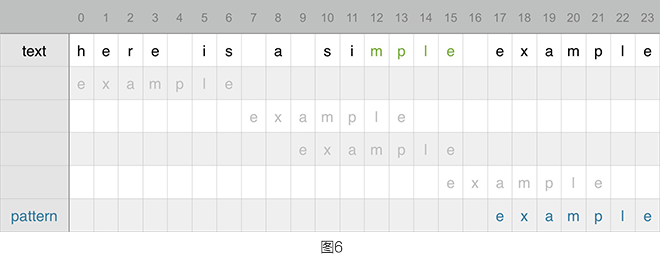
好了，移动的规则都讲完了，那么该直接上代码了，下面是使用 JavaScript 实现该算法的代码：

var boyerMoore = function( content, pattern, fromIndex ){
    var cLen = content.length,
        pLen = pattern.length,
        i = pLen - 1,
        badCharMap = {},
        goodSuffixMap = {},
        index, item, suffix, pre, j;

    fromIndex = fromIndex || i;

    for( ; i > 0; i-- ){
        item = pattern[i];

        // 创建坏字符规则表
        if( badCharMap[item] === undefined ){
            badCharMap[ item ] = i;
        }

        // 创建好后缀规则表
        suffix = pattern.slice( i );
        pre = pattern.slice( 0, i );

        if( suffix.length <= pre.length ){
            for( j = pre.length - 1; j >= 0; j-- ){
                item = pre.slice( j - suffix.length + 1, j + 1 );

                if( suffix === item ){
                    if( goodSuffixMap[suffix] === undefined ){
                        goodSuffixMap[suffix] = j - suffix.length + 1;
                    }
                }
            }
        }
    }

    var search = function( lastIndex ){
        var i = pLen - 1,   // 搜索字符串的索引标记
            j = lastIndex,  // 被搜索字符串的索引标记
            g = 0,  // 标记好后缀的长度
            badChar, goodSuffix, goodSuffixMove, badCharMove, badCharIndex, goodSuffixIndex;

        for( ; i > 0; i-- ){
            badChar = content[j];

            if( badChar === pattern[i] ){
                g++;
            }
            else{
                // 需要查找坏字符在搜索词上一次（lastIndexOf从右往左查找）的出现为止
                badCharIndex = badCharMap[ badChar ];

                if( badCharIndex === undefined ){
                    badCharIndex = -1;
                }

                badCharMove = i - badCharIndex;

                if( badCharMove <= 0 ){
                    badCharMove = 1;
                }

                // 如果存在好后缀，则计算好后缀可以移动的位置
                if( g ){
                    for( i = g; i > 0; i-- ){
                        goodSuffix = pattern.slice( 0 - i );

                        if( goodSuffix in goodSuffixMap ){
                            goodSuffixIndex = goodSuffixMap[ goodSuffix ];
                            goodSuffixMove = pLen - i - goodSuffixIndex;
                            break;
                        }
                    }

                    if( goodSuffixIndex === undefined ){
                        goodSuffixMove = pLen - g - 1;
                    }

                    // 取坏字符和好后缀规则中移动位数最大者
                    lastIndex += Math.max( goodSuffixMove, badCharMove );
                }
                else{
                    lastIndex += badCharMove;
                }

            /* 测试代码 start
                console.log( content );

                for( var i = 0, space = '', len = lastIndex - pLen + 1; i < len; i++ ){
                    space += ' ';
                }

                console.log( space + pattern );
                console.log( lastIndex );
                console.log( '-----------------------------' );
                测试代码 end */

                break;
            }

            j--;
        }

        if( pLen - 1 !== g ){
            // 已到末尾
            if( lastIndex + 1 > cLen ){
                index = -1;
            }
            // 没到末尾将继续搜索
            else{
                search( lastIndex );
            }
        }
        // 完全匹配
        else{
            index = lastIndex + 1 - pLen;
        }
    };

    search( fromIndex );
    return index;
};

var content = 'here is a simple example';
var query = 'example';

var index = boyerMoore( content, query );

console.log( 'boyerMoore : ' + index );
console.log( 'indexOf : ' + content.indexOf(query) );

本文算是对 阮一峰 的 字符串匹配的Boyer-Moore算法 补充和具体实现，也是我对 阮一峰 的文章中的算法思想的个人理解。对于坏字符的规则这个容易搞懂，但是好后缀容易搞不明白，他在那篇文章中感觉就在好后缀的计算规则上说的还不够清楚。

扩展阅读：Boyer-Moore字符串搜索算法